알고리즘 유형 정리

크루스칼알고리즘

크루스칼 알고리즘이란, 그래프로 이루어진 모든 정점들을 가장 적은 비용으로 연결하기 위한 방법 중 하나이다.

이때 제약조 건 중 하나는 그래프 내의 모든 정점들을 지날 때 사이클이 형성되면 안되는 조건이 포함된다.

따라서, 사이클을 형성하지 않고 모든 정점들을 최소 비용으로 지나는 상황을 구할 때 크루스칼 알고리즘을 사용한다.

이는 다른 표현으로 최소 신장 트리(Minimum Spanning Tree) 알고리즘이라고도 불리운다.

위의 용어들이 전문용어들이 있어 크게 와닿지가 않을 수 있다. 그래서 그냥 따분한 한 알고리즘 중 하나이지 않을가로 대수롭지 않게 여길 수 있겠지만, 현실의 적용부분으로 생각해보면 이해가 더 잘 될 수 있다.

예를들어 배민라이더가 5곳의 배달지역을 돌아야 한다면 어떤 경로로, 어떤 순서로 돌아야 가장 빠르게 돌 수 있을까 ?

이런 상황에서 필요한게 바로 최소 신장 트리 알고리즘인 것이다.

배민 라이더는 모든 배달지역을 한번씩 반드시 지나야 하며 , 이때 경로상의 거리대비 소요시간(비용)을 계산하여 가장 최소의 시간으로 모든 경로를 도는 추천 경로를 받아야지만 최대 이익으로 배달 임무를 완수할 수 있다.

물론 실제 배민이나 택배업체의 알고리즘은 더 고도화 된 알고리즘이겠지만 이해를 돕기 위해 예시를 들어보았다.

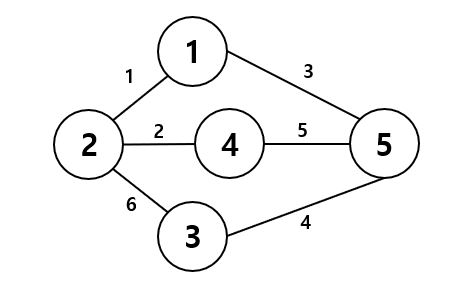
아래의 사진을 통해 실제 그래프의 예시를 확인해보도록 하자.

아래에는 정점과 간선의 가중치(비용)이 정의되어 있다.

크루스칼1

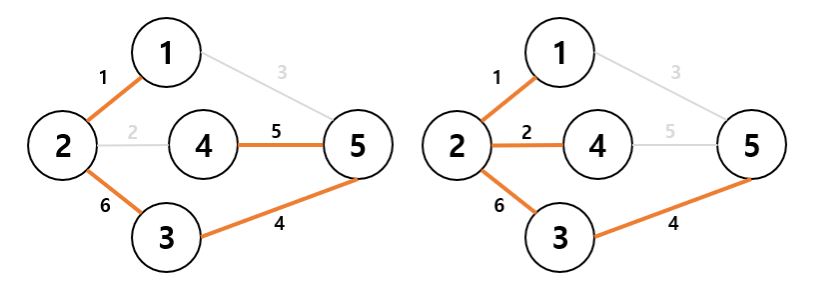
다양한 경로를 통해 다양한 신장 트리들을 만들 수 있다.

크루스칼2

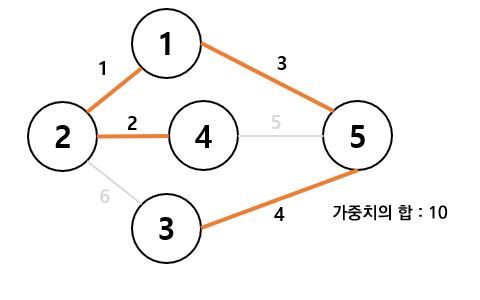
그 중 아래의 경우가 최소 가중치의 합을 나타내는 트리이고 이것이 최소 신장 트리가 되는 것이다.

크루스칼3

크루스칼 알고리즘 역시 위상정렬과 비슷한 그리디 알고리즘의 일원이다.

모든 간선들의 가중치를 오름차순으로 정렬한 뒤 가장 작은 가중치부터 하나씩 선택한다. 이때 신장 트리의 조건인 사이클 형성을 방지하는 조건만 신경써서 사이클이 형성되지 않는 경우에 한해 오름차순으로 선택하며 모든 정점들을 순회하면 된다.

가장 대중적으로 사이클 여부를 판단하는 방식은 Union&Find 자료구조를 사용하는 것이다.

Union&Find자료구조란?

서로 다른 두 집합을 병합하는 Union 연산을 수행하고, 집합의 원소가 어떤 집합에 속해 있는지 찾는 Find 연산을 하기 때문에 용어를 합쳐 사용하고 있다.

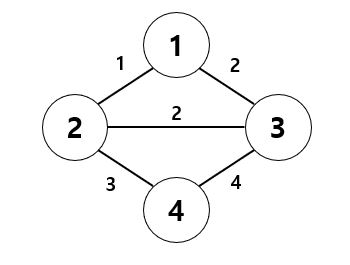
아래 예시를 통해 이해하고자 한다.

아래의 그래프에서는 정점들과 정점들간의 간선(가중치)가 존재한다. 모든 정점들은 각각 서로소의 집합으로 시작하며, 자신의 집합의 가장 헤더(부모) 노드가 어떤것인지 저장해야한다.

크루스칼4

parent 배열 |1|2|3|4| |-|-|-|-| |1|2|3|4|

parent 배열 |1|2|3|4| |-|-|-|-| |1|1|3|4|

parent 배열 |1|2|3|4| |-|-|-|-| |1|1|3|1|

다음 최소 간선은 2-4 간선이다. 하지만 2의 부모 노드는 1이고, 4의 부모노드 또한 1이기 때문에 Union 하지 않는다. 이런식으로 부모노드가 같지 않은 경우에 한해 Union 해 나간다면 사이클이 형성되지 않은 모든 노드를 연결 할 수 있다.

백준 예제 문제들을 통해 위에서 배운 크루스칼 알고리즘을 실전 연습해보도록 하자.

Reference
https://chanhuiseok.github.io/posts/algo-33/